ΕΛΛΗΝΙΚΗ ΑΡΙΘΜΟΛΟΓΙΑ
ΠΑΙΞΤΕ ΜΕ ΤΙΣ ΛΕΞΕΙΣ ΚΑΙ ΤΟΥΣ ΑΡΙΘΜΟΥΣ
Σε αυτή τη σελίδα μπορείτε να κάνετε τα εξής:
α. Να διαβάσετε το θεωρητικό υπόβαθρο και μετά να κάνετε το τεστ.
β. Να διαβάσετε το σπουδαιότερο κομμάτιγια την Ελληνική Γλώσσα, τον χρυσό αριθμό φ, και μια νέα αριθμολογική θεωρία και μετά να κάνετε το τεστ
γ. Να κάνετε κατευθείαν το τεστ, επιλέγοντας στο επόμενο πλαίσιο ποιον τρόπο επιθυμείτε. Ο πρώτος είναι ο κλασσικός (προτείνεται) και ο δεύτερος είναι ο σύγχρονος, για την ερμηνεία του οποίου όμως πρέπει πρώτα να διαβάσετε τη θεωρία.
Τί θέλετε να κάνετε από τα δύο;
|
Θέλω να ελέγξω τη σχέση μεταξύ: |
|
|
(Μπορεί να ανήκει στο ίδιο φύλο, αν πρόκειται για φιλία ή συνεργασία)
Μόλις δώσετε τα στοιχεία σας, πατήστε "Υπολογισμός" και μετακινηθείτε παρακάτω για να δείτε τα αποτελέσματα
Χώρος εμφάνισης αποτελεσμάτων
Αριθμολογία είναι η μελέτη της μυστικής σχέσης μεταξύ ενός αριθμού ή μέτρησης και της ζωής. Διαθέτει πολλά συστήματα, παραδόσεις και πεποιθήσεις. Η αριθμολογική μαντεία με συστήματα όπως η "ισοψηφία" ήταν δημοφιλής μεταξύ των πρώτων μαθηματικών, όπως ο Πυθαγόρας, αλλά δεν θεωρείται πλέον ως "επίσημα μαθηματικά" από τους σύγχρονους επιστήμονες.
Σήμερα, η αριθμολογία συνδέεται συχνά με το παραφυσικό, παράλληλα με την αστρολογία και άλλες παρόμοιες μαντικές τεχνικές.
Ο όρος μπορεί επίσης να χρησιμοποιηθεί για εκείνους που διαθέτουν ιδιαίτερη πίστη στα αριθμητικά μοτίβα, ακόμη και αν αυτοί οι άνθρωποι δεν ασκούν την παραδοσιακή αριθμολογία. Για παράδειγμα, ο μαθηματικός Underwood Dudley, το 1997, στο βιβλίο του "Αριθμολογία ή τι πίστευε ο Πυθαγόρας" χρησιμοποιεί τον όρο για να περιγράψει πρακτικές εφαρμογής της κυματικής αρχής Ελιοτ στην ανάλυση της αγοράς μετοχών.
Επιστροφή στην αρχή της σελίδας
Ιστορία
Η σύγχρονη αριθμολογία συχνά περιέχει πτυχές όλων των αρχαίων πολιτισμών και δασκάλων, μεταξύ των οποίων οι Βαβυλώνιοι, ο Πυθαγόρας και οι οπαδοί του, η αστρολογική φιλοσοφία από την ελληνιστική Αλεξάνδρεια, ο παλαιοχριστιανικός μυστικισμός, οι πρώιμοι Γνωστικοί, το Εβραϊκό σύστημα της Καμπάλα, οι ινδικές Βέδες, ο κινεζικός "Κύκλος των Νεκρών", και το αιγυπτιακό «Βιβλίο των Αρχόντων του Μυστικής Αίθουσας".
Ο Πυθαγόρας και άλλοι φιλόσοφοι της εποχής του πίστευαν ότι επειδή οι μαθηματικές έννοιες ήταν πιο «πρακτικές» (πιο εύκολο να ρυθμιστούν και να ταξινομηθούν είχαν και μεγαλύτερη ακρίβεια. Ωστόσο, ο Πυθαγόρας δεν έπλασε ο ίδιος το σύστημα που αποκαλείται αριθμολογία. Αυτός απλά άνοιξε το δρόμο για την θεώρηση των αριθμών ως αρχέτυπα και όχι απλούς αριθμούς.
Ο Αγ. Αυγουστίνος Ιππώνος ή ιερός Αυγουστίνος (354-430 μ.Χ.) έγραψε: «Οι αριθμοί είναι η παγκόσμια γλώσσα που δόθηκε από το Θεό στον άνθρωπο ως επιβεβαίωση της αλήθειας." Παρόμοια με τον Πυθαγόρα, κι αυτός πίστευε ότι όλα είχαν αριθμητικές σχέσεις και επαφίεται στο ανθρώπινο μυαλό να αναζητήσει και να διερευνήσει τα μυστικά αυτών των σχέσεων ή να αποκαλυφθούν από την θεία χάρη.
Το 325 μ.Χ., μετά την Πρώτη Σύνοδο της Νίκαιας, οι διαφοροποιήσεις από τις πεποιθήσεις της Εκκλησίας χαρακτηρίστηκαν ως αιρέσεις στο εσωτερικό της Ρωμαϊκής Αυτοκρατορίας. Η αριθμολογία δεν αντιμετωπίστηκε με εύνοια από τις χριστιανικές αρχές της εποχής και εξοβελίστηκε στη σφαίρα των μη εγκεκριμένων πεποιθήσεων μαζί με την αστρολογία και άλλες μορφές μαντείας και τη "μαγεία". Παρά το γεγονός αυτού του θρησκευτικού εξαγνισμού, η πνευματική σημασία που αποδιδόταν ως τότε σε κάποιους "ιερούς αριθμούς", δεν εξαφανίστηκε. Για παράδειγμα υπάρχουν πολλοί αριθμοί όπως ο "αριθμός του Ιησού», ή ο "αριθμός του Διαβόλου" που σχολιάστηκε και αναλύθηκε από τον Δωρόθεο της Γάζας ενώ η αριθμολογία εξακολουθεί να χρησιμοποιείται τουλάχιστον από κάποιους συντηρητικούς Ορθόδοξους Ελληνικούς κύκλους.
Η αριθμολογία είναι εμφανής σε όλο το έργο του Sir Thomas Browne του 1658, "Ο Κήπος του Κύρου". Στις σελίδες του ο συγγραφέας επιχειρεί να αποδείξει ότι ο αριθμός πέντε και το σχετικό χιαστί σχέδιο εντοπίζεται σε όλες τις τέχνες, στον στο σχεδιασμό και στη φύση - ιδιαίτερα τη βοτανολογία.
Η σύγχρονη αριθμολογία έχει διάφορες επιρροές. Το βιβλίο της Ruth A. Drayer , "Αριθμολογία, η ισχύς των αριθμών", λέει ότι στις αρχές του 20ου αι., η Dow Balliett συνδύασε το έργο του Πυθαγόρα με διάφορες βιβλικές αναφορές. Στη συνέχεια, η μαθήτρια της Balliet, δρ. Juno Jordan, στις 23 Οτωβρίου 1972, άλλαξε περαιτέρω την αριθμολογία και βοήθησε να γίνει το σύστημα που είναι γνωστό σήμερα με τον τίτλο «Πυθαγόρειο», αν και ο Πυθαγόρας ο ίδιος δεν είχε καμία σχέση αυτό.
Επιστροφή στην αρχή της σελίδας
Ορισμοί των αριθμών
Δεν υπάρχει κάποια στάνταρ ερμηνεία για το τι σημαίνει και τι αντιπροσωπεύει ο κάθε αριθμός Εντούτοις σε γενικές γραμμές, αυτό που θεωρείαι κοινά αποδεκτό, ιδιαίτερα στη δυτική προσέγγιση είναι το εξής:
1= Ατομικότητα, Επιθετικότητα, Κινεζικό Γιάνγκ
2= Ισορροπία, Ένωση, Δεκτικότητα, Κινεζικό Γιν
3= Επικοινωνία / αλληλεπίδραση, Ουδετερότητα
4= Δημιουργία
5= Δράση, Ανησυχία
6= Αντίδραση / ροή, Ευθύνη
7= Σκέψη / συνείδηση
8= Ισχύς / θυσία
9= Υψηλότερο επίπεδο αλλαγής
Επιστροφή στην αρχή της σελίδας
Αλφαβητικά συστήματα
Υπάρχουν πολλά αριθμολογικά συστήματα που αναθέτουν αριθμητικές τιμές στα γράμματα της αλφαβήτου. Ορισμένα από αυτά είναι τα ψηφία abjad στα αραβικά, οι εβραϊκοί αριθμοί, το αρμενικό σύστημα, το ελληνικό σύστημα κλπ. Η πρακτική ανάθεσης μυστικιστικής σημασίας στις λέξεις, με βάση τις αριθμητικές τιμές τους, καθώς και οι συσχετισμοί μεταξύ λέξεων ίσης αξίας, που είναι γνωστή ως Γεματρία ή Ισοψηφία. Ο όρος είναι εβραϊκή δάνεια λέξη, και πιστεύεται ότι προέρχεται από την ελληνική λέξη «γεωμετρία» ή «γραμματεία», αν και η ετυμολογία του δεν είναι γνωστή.
Όπως και στα Ελληνικά, στα Εβραϊκά κάθε γράμμα του αλφαβήτου έχει τη δική του αριθμητική αξία. Η Γεματρία αφορά στον υπολογισμό της αριθμητικής ισοδυναμίας των γραμμάτων, των λέξεων ή των φράσεων με απώτερο σκοπό την κατανόηση του αλληλοσυσχετισμού των γραμμάτων και την αποκωδικοποίηση κρυμμένων ιδεών. Αυτή η αντίληψη προέρχεται από την άποψη ότι εφόσον —σύμφωνα με τις Εβραϊκές Γραφές— όλος ο κόσμος δημιουργήθηκε με το «λόγο» του Θεού, θα πρέπει αντίστοιχα το κάθε γράμμα να αναπαριστά μια διαφορετική δημιουργική δύναμη. Κατ' αυτό τον τρόπο, τα αριθμητικά ισοδύναμα των λέξεων συνδέονται με τη δημιουργική δυναμική που πιστεύεται ότι κατέχουν.
Οι Πυθαγόριοι, επίσης, έκαναν χρήση των γραμμάτων της Ελληνικής για να καταγράψουν γεωμετρικούς συμβολισμούς, ήχους και αριθμούς.
Όπως είναι γνωστό στην ελληνική γλώσσα το ελληνικό αριθμολογικό σύστημα είχε την εξής διάταξη:
α΄ β΄ γ΄ δ΄ ε΄ ϛ΄ ζ΄ η΄ θ΄ είναι οι αριθμοί 1 2 3 4 5 6 7 8 9 αντίστοιχα
ι΄ κ΄ λ΄ μ΄ ν΄ ξ΄ ο΄ π΄ ϟ΄ είναι οι αριθμοί 10 20 30 ... 90 αντίστοιχα
ρ΄ σ΄ τ΄ υ΄ φ΄ χ΄ ψ΄ ω΄ ϡ΄ είναι οι αριθμοί 100 200 300 ... 900 αντίστοιχα
Έτσι κάθε λέξη φέρει μια αριθμητική αξία, η οποία αθροίζεται για να μετατραπεί σε έναν αριθμό από το 1 ως το 9.
Παραδείγματα:
3489 → 3 + 4 + 8 + 9 = 24 → 2 +4 = 6
Καλημέρα → 20+1+30+8+40+5+100+1= 205 → 2 +0+ 5 = 7
Ένας πιο γρήγορος τρόπος για να καταλήξουμε σε ένα μονοψήφιο άθροισμα (ή ψηφιακή ρίζα) επιτυγχάνεται απλά εάν βρούμε το υπόλοιπο της διαίρεσης του αριθμού με το 9, και στην περίπτωση που είναι 0 το αντικαθιστούμε με το 9. Δηλαδή στα παραπάνω παραδείγματα 3489:9=387 και υπόλοιπο 6 ή 205:9=22 και υπόλοιπο 7
Επιστροφή στην αρχή της σελίδας
Πυθαγόρειο σύστημα
Ο Πυθαγόρας δεν συμμετείχε ποτέ στα συστήματα αριθμολογίας που είναι γνωστά στις μέρες μας. Ήταν ένας φιλόσοφος που συνέβαλε στην κατανόηση της έννοιας των αριθμών ως σύμβολα παρά ως απλούς αριθμούς. Η αριθμολογία όπως την ξέρουμε είναι ένα σύστημα που βασίζεται στην Γεματρία, η οποία είναι αποτελεί έναν Καβαλιστικό κλάδο.
Αριθμολογία και αστρολογία
Μερικοί αστρολόγοι πιστεύουν ότι κάθε αριθμός από το 0 έως 9 κυβερνάται από ένα ουράνιο σώμα στο ηλιακό μας σύστημα.
Αριθμολογία και αλχημεία
Πολλές αλχημικές θεωρίες ήταν στενά συνδεδεμένες με την αριθμολογία. Ο Πέρσης αλχημιστής Τζαμπίρ Ιμπν Χαγιάν εφευρέτης πολλών χημικών διεργασιών που εξακολουθούν να χρησιμοποιούνται και σήμερα, πλαισίωνε τα πειράματά του με μια πολύπλοκη αριθμολογία στη βάση των ονομάτων των ουσιών στην αραβική γλώσσα.
Η αριθμολογία στα τυχερά παιχνίδια
Ορισμένοι παίκτες εφαρμόζουν μεθόδους που μερικές φορές αποκαλούνται αριθμολογικές σε παιχνίδια που περιλαμβάνουν αριθμούς, όπως το μπίνγκο, η ρουλέτα, το ΚΙΝΟ ή τα λαχεία. Παρά το γεγονός ότι δεν μπορεί να εφαρμοστεί καμία στρατηγική για να αυξηθούν οι πιθανότητες σε τέτοια παιχνίδια, οι παίκτες τείνουν να χρησιμοποιούν "τυχερούς αριθμούς" για να εντοπίσουν αυτόν που νομίζουν ότι θα τους βοηθήσει. Δεν υπάρχουν στοιχεία ότι οποιαδήποτε τέτοια «αριθμολογική στρατηγική" δίνει καλύτερα αποτελέσματα από την καθαρή τύχη, αλλά οι μέθοδοι μερικές φορές ενθαρρύνονται, π.χ. από τους ιδιοκτήτες των καζίνο.
Η αριθμολογία στην επιστήμη
Κάποιες επιστημονικές θεωρίες μερικές φορές ονομάζονται "αριθμολογίες" όταν η αρχική τους έμπνευση εδράζεται σε ένα σύνολο επαναλαμβανόμενων μοτίβων και όχι σε επιστημονικές παρατηρήσεις. Η χρήση του όρου είναι αρκετά κοινή στους κόλπους της επιστημονικής κοινότητας και χρησιμοποιείται ως επί το πλείστον για να απορριφθεί μια θεωρία επιστημονικά αμφισβητήσιμη.
Το πιο γνωστό παράδειγμα "αριθμολογίας" στην επιστήμη είναι η συμπτωματική ομοιότητα ορισμένων μεγάλων αριθμών που κέντρισαν το ενδιαφέρον, σπουδαίων επιστημόνων όπως ο μαθηματικός φυσικός Paul Dirac, ο μαθηματικός Hermann Weyl και ο αστρονόμος Arthur Stanley Eddington. Αυτές οι αριθμητικές "συμπτώσεις" αναφέρονται σε ποσότητες όπως ο λόγος της ηλικίας του σύμπαντος προς την ατομική μονάδα του χρόνου, ο αριθμός των ηλεκτρονίων στο σύμπαν, και η διαφορά ανάμεσα στις δυνάμεις της βαρύτητας και της ηλεκτρικής δύναμης του ηλεκτρονίου και του πρωτονίου.
Η ανακάλυψη των ατομικών τριάδων (που αφορούν τα στοιχεία που ανήκουν στην ίδια ομάδα ή στήλη του περιοδικού πίνακα) θεωρήθηκε ως μια μορφή αριθμολογίας, και η οποία όμως τελικά οδήγησε στην κατασκευή του περιοδικού πίνακα. Στην περίπτωση αυτή το ατομικό βάρος του ελαφρύτερου και του βαρύτερου στοιχείου αθροίζονται, και ο μέσος όρος τους είναι πολύ κοντά στο ατομικό βάρος του ενδιάμεσου στοιχείου. Αν και αυτό δεν λειτουργεί με κάθε τριπλέτα της ίδιας ομάδας, εντούτοις δούλεψε πολύ καλά και επέτρεψε α0γότερα στους επιστήμονες να κάνουν γενικεύσεις.
Οι συνυπάρξεις μεγάλων αριθμών, συνεχίζουν να συναρπάζουν πολλούς μαθηματικούς φυσικούς. Για παράδειγμα, ο James G. Gilson έχει κατασκευάσει μια «κβαντική θεωρία της βαρύτητας" που βασίζεται χαλαρά στις υπόθεση του Dirac περί μεγάλων αριθμών.
Επίσης ο Wolfgang Pauli γοητεύτηκε επίσης από την εμφάνιση ορισμένων αριθμών, συμπεριλαμβανομένου του 137, στη φυσική.
Ο αριθμός Φ
Μια σπουδαία αριθμολογική προσέγγιση ή οποία έχει σαφές επιστημονικό υπόβαθρο είναι ο χρυσός αριθμός φ, ή όπως αλλιώς λέγεται η χρυσή αναλογία.
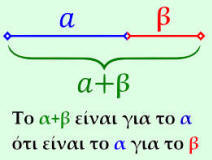 Ως χρυσή τομή φ ορίζεται ως το πηλίκο των θετικών αριθμών α και β όταν ισχύει α/β=(α+β)/α και ισούται περίπου με 1,618. Θεωρείται ότι δίνει αρμονικές αναλογίες και για το λόγο αυτό έχει χρησιμοποιηθεί στην αρχιτεκτονική και τη ζωγραφική, τόσο κατά την αρχαία Ελλάδα όσο και κατά την Αναγέννηση. Η χρυσή τομή συμβολίζεται με το γράμμα φ προς τιμήν του Φειδία, του γνωστότερου ίσως γλύπτη της ελληνικής αρχαιότητας, και του σημαντικότερου της κλασικής περιόδου.
Ως χρυσή τομή φ ορίζεται ως το πηλίκο των θετικών αριθμών α και β όταν ισχύει α/β=(α+β)/α και ισούται περίπου με 1,618. Θεωρείται ότι δίνει αρμονικές αναλογίες και για το λόγο αυτό έχει χρησιμοποιηθεί στην αρχιτεκτονική και τη ζωγραφική, τόσο κατά την αρχαία Ελλάδα όσο και κατά την Αναγέννηση. Η χρυσή τομή συμβολίζεται με το γράμμα φ προς τιμήν του Φειδία, του γνωστότερου ίσως γλύπτη της ελληνικής αρχαιότητας, και του σημαντικότερου της κλασικής περιόδου.
Ο χρυσός λόγος όπως είπαμε ήταν γνωστός στους Πυθαγόρειους. Στο μυστικό τους σύμβολο, την πεντάλφα, ο χρυσός λόγος εμφανίζεται στις πλευρές του αστεριού. Με βάση το χρυσό λόγο δημιουργήθηκαν πολλά έργα της κλασσικής εποχής, όπως ο Παρθενώνας, και της αναγεννησιακής εποχής, όπως είναι ζωγραφικά έργα του Λεονάρντο ντα Βίντσι. Ακόμη και σήμερα χρησιμοποιείται για την απόδοση της αρμονίας σε έργα, ή στην πλαστική χειρουργική για την ωραιοποίηση του ανθρώπινου προσώπου.
 Το Φ στην αρχιτεκτονική
Το Φ στην αρχιτεκτονική
Η πρόσοψη του Παρθενώνα αποτελεί ένα παράδειγμα χρήσης της χρυσής τομής (Φ) στην αρχιτεκτονική. Ο τριγωνισμός, μια άλλη μέθοδος συγκρότησης ρυθμικών καμβάδων με βάση ορισμένα προνομιούχα τρίγωνα, γνώρισε τη μεγαλύτερη διάδοσή του τον περασμένο αιώνα. Αυτά είναι: (1)το πυθαγόρειο, δηλαδή το ορθογώνιο με σχέση πλευρών 3:4:5, (2) το αιγυπτιακό, δηλαδή το ισοσκελές με αναλογία βάσης προς ύψος 8:5, (3) το ισοσκελές με γωνία κορυφής 36 μοίρες, που αποτελεί τη μονάδα του κανονικού δεκαγώνου, και έχει σχέση πλευράς προς βάση Φ και τέλος (4) το ισόπλευρο, που αποτελεί τη μονάδα του εξαγώνου. Τέτοιες μεθόδους επαλήθευσης συναντά κανείς στα αρχιτεκτονικά έργα του μοντέρνου κινήματος, Le Corbusier, Bauhaus κλπ.
Το Φ στην τέχνη
Αργότερα ο Leonardo Da Vinci ζωγράφισε το πρόσωπο της Mona Lisa ώστε αυτό να χωράει τέλεια σε ένα χρυσό ορθογώνιο και δόμησε τον υπόλοιπο πίνακα γύρω από το πρόσωπο χωρίζοντάς τον επίσης σε χρυσά ορθογώνια. Ο Mozart διαίρεσε μεγάλο αριθμό από τις σονάτες του σε δύο μέρη, η χρονική αναλογία των οποίων αντιστοιχεί στη χρυσή τομή, τον αριθμό φ, αν και υπάρχει σημαντική διχογνωμία για το κατά πόσο αυτό έγινε σκόπιμα.
.jpg) Το Φ στη φύση
Το Φ στη φύση
Το ανθρώπινο σώμα έχει δομηθεί και αναπτύσσεται σε αναλογίες Φ. Δεν είναι τυχαίο ότι πολλές «ανατολίτικες θρησκείες» και κινήματα στα πλαίσια της διδασκαλίας τους για διαλογισμό και την «αυτοσυγκέντρωση και στο λεγόμενο «γιόγκα» η στάση του ανθρώπινου σώματος γίνεται κατά αυτό τον τρόπο έτσι ώστε τα «κεντρικά - κομβικά» σημεία του σώματος να βρίσκονται σε αναλογίες Φ. Αν θέλει κανείς να δει ένα χρυσό ορθογώνιο αρκεί να κοιτάξει μια πιστωτική κάρτα το σχήμα της οποίας είναι ακριβώς αυτό. Τέλος υπάρχουν καταγραφές που μιλούν για την ύπαρξη του Φ στην δομή του DNA.
Αν μετρήσουμε τις μέλισσες σε μια κυψέλη οπουδήποτε στον κόσμο θα παρατηρήσουμε ότι η αναλογία των θηλυκών προς των αρσενικών μελισσών καταλήγει πάντα σε έναν αριθμό... Αν μετρήσουμε την απόσταση από την κορυφή του κεφαλιού μέχρι το πάτωμα και τη διαιρέσουμε με την απόσταση από τον αφαλό μέχρι το πάτωμα προκύπτει πάντα ο ίδιος αριθμός...
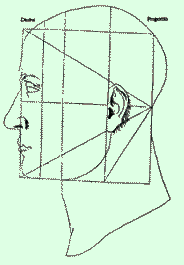 Αν μετρήσουμε την απόσταση από τον ώμο μέχρι τις άκρες των δακτύλων και τη διαιρέσουμε με την απόσταση από τον αγκώνα μέχρι τις άκρες των δακτύλων προκύπτει πάντα ο ίδιος αριθμός... ο αριθμός αυτός είναι ο 1,618 ή ο γνωστός αριθμός φ!!! Στο ανθρώπινο σώμα ο χρυσός λόγος εντοπίζεται σε πολλές ανατομικές αναλογίες, τις οποίες παρατήρησε και κατέγραψε ο Λεονάρντο ντα Βίντσι στον βιτρούβιο άντρα.
Αν μετρήσουμε την απόσταση από τον ώμο μέχρι τις άκρες των δακτύλων και τη διαιρέσουμε με την απόσταση από τον αγκώνα μέχρι τις άκρες των δακτύλων προκύπτει πάντα ο ίδιος αριθμός... ο αριθμός αυτός είναι ο 1,618 ή ο γνωστός αριθμός φ!!! Στο ανθρώπινο σώμα ο χρυσός λόγος εντοπίζεται σε πολλές ανατομικές αναλογίες, τις οποίες παρατήρησε και κατέγραψε ο Λεονάρντο ντα Βίντσι στον βιτρούβιο άντρα.
Πού αλλού συναντάμε τον αριθμό αυτό; Στον αριθμό της σπείρας που μπορούμε να μετρήσουμε αριστερά και δεξιά στους σπόρους των ηλίανθων, στον αριθμό των πετάλων των λουλουδιών (3 στο αγριόκρινο, 5 ή 8 σε κάποια φυτά του γένους ranunculus, ενώ οι μαργαρίτες και οι ηλίανθοι συνήθως έχουν 13, 21, 34, 55 ή 85 πέταλα...) και στον αριθμό των ανθών στα σπιράλ του κουνουπιδιού και του μπρόκολου.
Επίσης, στον ναυτίλο (ένα πανέμορφο κοχύλι), ο λόγος των ακτινών του κάθε θαλάμου με τον προηγούμενο ισούται με το χρυσό λόγο.
 Για ποιο λόγο άραγε η φύση δείχνει ιδιαίτερη αδυναμία στην ακολουθία των αριθμών που ο λόγος τους μας δίνει το φ (ακολουθία Φιμπονάτσι); Τα φύλλα, τα πέταλα και οι σπόροι οργανώνονται στα φυτά ακολουθώντας ένα συγκεκριμένο μοτίβο γιατί έτσι, καθώς αναπτύσσονται, αξιοποιούν με τον καλύτερο δυνατό τρόπο το διαθέσιμο χώρο. Αν κατανείμουμε τα φύλλα στο μίσχο σύμφωνα με το χρυσό αριθμό, όλα θα επωφελούνται στο μέγιστο βαθμό από το φως του ήλιου, χωρίς να κρύβει το ένα το άλλο. Τα λουλούδια, χάρη στο χρυσό αριθμό, προσελκύουν όσο το δυνατόν καλύτερα τα έντομα που μεταφέρουν τη γύρη. Η ακολουθία Φιμπονάτσι είναι η πιο επιτυχημένη προσέγγιση του αριθμού φ.
Για ποιο λόγο άραγε η φύση δείχνει ιδιαίτερη αδυναμία στην ακολουθία των αριθμών που ο λόγος τους μας δίνει το φ (ακολουθία Φιμπονάτσι); Τα φύλλα, τα πέταλα και οι σπόροι οργανώνονται στα φυτά ακολουθώντας ένα συγκεκριμένο μοτίβο γιατί έτσι, καθώς αναπτύσσονται, αξιοποιούν με τον καλύτερο δυνατό τρόπο το διαθέσιμο χώρο. Αν κατανείμουμε τα φύλλα στο μίσχο σύμφωνα με το χρυσό αριθμό, όλα θα επωφελούνται στο μέγιστο βαθμό από το φως του ήλιου, χωρίς να κρύβει το ένα το άλλο. Τα λουλούδια, χάρη στο χρυσό αριθμό, προσελκύουν όσο το δυνατόν καλύτερα τα έντομα που μεταφέρουν τη γύρη. Η ακολουθία Φιμπονάτσι είναι η πιο επιτυχημένη προσέγγιση του αριθμού φ.
Επιστροφή στην αρχή της σελίδας
Όλες οι παραπάνω πληροφορίες προέρχονται κυρίως από την Wikipedia, αλλά και κάποια ελληνικά σάιτ και τις μετέφρασα, έτσι ώστε να πάρετε μια ιδέα για το τι εστί Αριθμολογία. Εντούτοις θα πρέπει να κάνουμε ορισμένες επισημάνσεις για τον τρόπο με τον οποίο αντιμετωπίζεται αυτό το ζήτημα στην παρούσα ιστοσελίδα.
Αρχικά είχα αρχίσει να ψάχνω να βρω ένα ακόμη τεστ καθώς το σάιτ δέχεται πλέον πάρα πολλές επισκέψεις και ό,τι έχει να κάνει με προβλέψεις, συσχετισμούς και εξερεύνηση του αγνώστου είναι πολύ "πιασάρικο". Η αριθμολογία ανήκει σε αυτούς τους τομείς, όμως έπρεπε να είναι κάτι εξαιρετικά πρωτότυπο για να διασωθεί και η... φήμη μου.
Σκέφτηκα, λοιπόν, ότι η αριθμολογία με βάση τις αρχές του Πυθαγόρα δεν ήταν και τόσο "επιστημονική". Δηλαδή η αντιστοιχία αριθμών και γραμμάτων ήταν μια "αυθαίρετη" κατασκευή, καθώς οι αρχαίοι απλά πήραν το πρώτο γράμμα και συμβόλισαν το 1, το δεύτερο για το 2 και ούτω καθεξής. Παρ' όλο που η αντιστοιχία αυτή εδραιώθηκε βαθιά στα σχεδόν 3000 χρόνια της ιστορίας του ελληνικού γραπτού λόγου, δεν παύει να είναι αυθαίρετη νοητική κατασκευή όπως και στην αγγλική αριθμολογία. (Γκουγκλάρετε το numerology για περισσότερες πληροφορίες).
Πώς θα μπορούσε όμως να αποδοθεί σε κάθε γράμμα ένας αριθμός, που να είναι αληθινά αντιπροσωπευτικός κάποιου πράγματος σε σχέση με την ίδια τη γλώσσα;
Εδώ ήρθε σε βοήθειά μου η πρόοδος της τεχνολογίας. Υπάρχει μια ιστοσελίδα (https://invokeit.wordpress.com/frequency-word-lists/) στην οποία καταγράφεται η συχνότητα των 50.000 πιο χρησιμοποιούμενων λέξεων σε κάθε γλώσσα, όπως αυτές εμφανίζονται στους μεταφρασμένους υπότιτλους διάφορων ταινιών!
Εγώ πήρα τις 10.000 πρώτες από τις βασικότερες γλώσσες και μπήκα στην εξής διαδικασία: Μέτρησα πόσα "α", υπάρχουν στην ελληνική γλώσσα, πόσα "β", πόσα "γ" και ούτω καθεξής. Η συχνότητα χρήσης των γραμμάτων, αν μη τι άλλο, είναι ένα πολύ μετρήσιμο μέγεθος. Έτσι, βάζοντας τις λέξεις στο Excel, πήρα τα εξής αποτελέσματα:
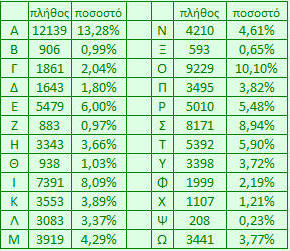
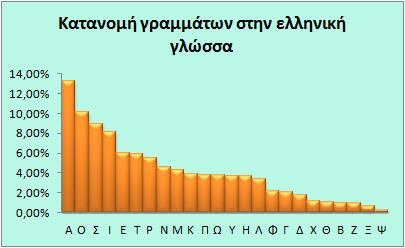
Όπως βλέπετε, το Α είναι το "σπουδαιότερο" γράμμα γιατί χρησιμοποιείται πολύ συχνά στα ελληνικά, σε ποσοστό 13,28%, ακολουθεί το Ο με ποσοστό 10,10% και ούτω καθ' εξής. Οπότε τώρα έχουμε κάτι "χειροπιαστό" για να αποδώσουμε μια αριθμητική τιμή σε κάθε γράμμα. Έναν αριθμό δηλαδή, που εκφράζει πόσο σημαντικό είναι το κάθε γράμμα στη γλώσσα που χρησιμοποιείται. Και όπως είναι φυσικό, σε κάθε γλώσσα, διαφέρει. Τη δουλειά αυτή την είχαν κάνει κάποιοι άλλοι ήδη για τα Αγγλικά, τα Γαλλικά, τα Γερμανικά κλπ, εντούτοις για τα Ελληνικά δεν βρήκα τίποτα στο διαδίκτυο, οπότε μπορεί κάλλιστα η δική μου παρέμβαση να θεωρηθεί "πρωτότυπη" και να με αναφέρουν στη διεθνή βιβλιογραφία στο μέλλον!!!
Να σημειωθεί ωστόσο ότι επειδή οι μετρήσεις αυτές αφορούν μόνο τις 10.000 λέξεις της παραπάνω ιστοσελίδας, σίγουρα τα ποσοστά στο σύνολο της γλώσσας θα είναι λίγο διαφορετικότερα, αλλά οπωσδήποτε δεν θα υπάρχουν στατιστικά σημαντικές διαφορές. Δεν υπήρχε δυνατότητα ελέγχου των υπόλοιπων εξαιτίας της υπολογιστικής ισχύος που απαιτούνταν και με τον απλό οικιακό υπολογιστή δεν είναι τόσο εύκολο να γίνουν, καθώς κολλούσε το excel.
Επιστροφή στην αρχή της σελίδας
Ας δούμε τι γίνεται με τις άλλες γλώσσες.
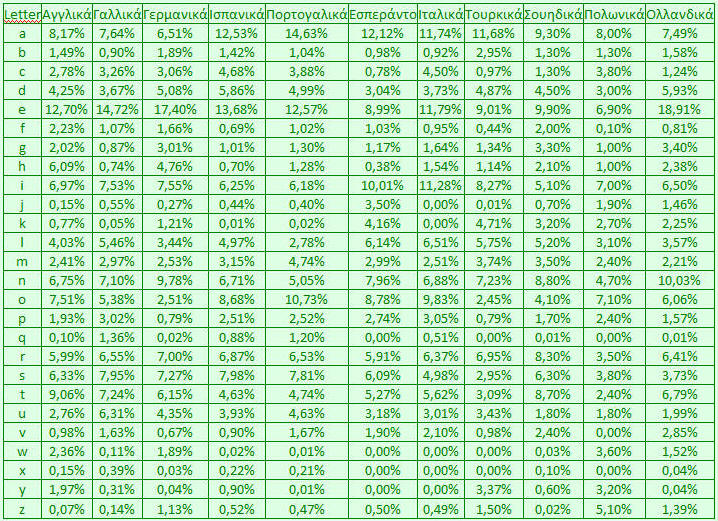
Πηγή: Wikipedia
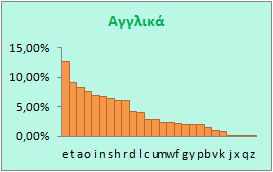
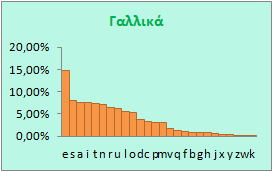
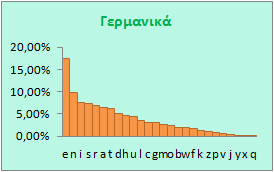
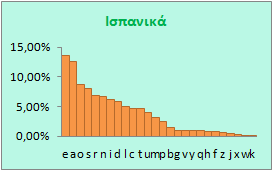
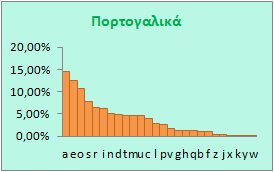
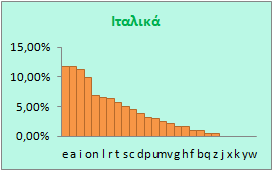
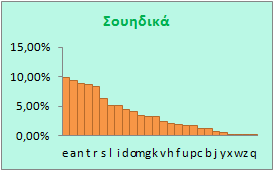
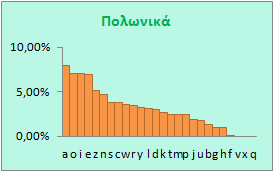
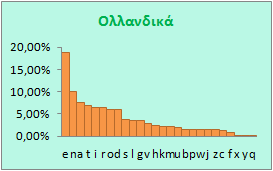
Όπως βλέπετε σε κάθε γλώσσα η συχνότητα χρήσης των γραμμάτων είναι διαφορετική. Ακόμη και στα Ισπανικά και τα Ιταλικά υπάρχουν διαφορές, παρ' όλο που οι γλώσσες είναι σχεδόν ίδιες, γεγονός βέβαια που πρέπει να οφείλεται σε κλιματικές αιτίες, σε ιστορικούς λόγους, ακόμη και σε λόγους ιδιοσυγκρασίας των ομιλούντων τις διάφορες γλώσσες, η οποία διαμορφώνεται από ένα πλήθος παραγόντων.
Ωραία ως εδώ. Τι σημαίνουν όμως όλα αυτά; Πώς μπορούν να βοηθήσουν στην εξαγωγή κάποιων συμπερασμάτων σε σχέση με τη δομή της γλώσσας και κάποιας σύνδεσής της με το βαθύτερο νόημα της ανθρώπινης ύπαρξης ή μιας υποβόσκουσας δύναμης των αριθμών μέσα στις λέξεις;
Κατ' αρχάς, ας πάρουμε ένα παράδειγμα, όπως η λέξη "πατέρας". Δίνοντας σε κάθε γράμμα την αξία που έχει ως ποσοστό έχουμε τα εξής: π=3,82 | α=13,28 | τ=5,90 | ε=6,00 | ρ=5,48 | α=13,28 | σ=8,94.
Το άθροισμα είναι 3,82+13,28+5,9+6+5,48+13,28+8,94 = 56,7. Άρα η λέξη "πατέρας" έχει ένα, ας το πούμε, "λεξαριθμικό βάρος" ίσο με 56,7. Αντίστοιχα η λέξη "μητέρα" χει βάρος 38,61, η λέξη "Θανάσης" έχει βάρος 53,74 και ούτω καθ' εξής. (Στο πάνω μέρος αυτής της σελίδας υπάρχει ένα πρόγραμμα που βρίσκει όχι μόνο τα βάρη των λέξεων ή των εκφράσεων αλλά και ένα πλήθος άλλων χαρακτηριστικών τους, από αυτά που θα περιγράψουμε στη συνέχεια). Μια πρώτη ιδέα είναι να ψάξουμε να βρούμε λέξεις με παρόμοια βάρη, οι οποίες όπως θα υπέθετε κανείς θα μπορούσε να έχουν κάποια συνάφεια σε μεταφυσικό επίπεδο.
Από τις συνολικά 10.000 ελληνικές λέξεις που είχα στη διάθεσή μου, εντόπισα 2253 που έχουν μοναδικό λεξαριθμικό βάρος, - πάρα πολλές για να βγει κάποιο συμπέρασμα - ενώ και από τις υπόλοιπες, περίπου μόνο ανά δύο ή τρεις έχουν το ίδιο βάρος. Από έναν πρόχειρο έλεγχο φάνηκε ότι οι λέξεις που είχαν το ίδιο βάρος δεν συνδέονται με κάποιο εσωτερικό τρόπο. Επίσης τα μεγέθη των βαρών στη συντριπτική τους πλειοψηφία ξεπερνούσαν το 10, που συνήθως αποτελεί τη βάση για οποιαδήποτε "παραδοσιακή" αριθμολογική ανάλυση. (Θα ήταν σπουδαίο εύρημα αν π.χ. ο "πατέρας" και η "μητέρα" είχαν το ίδιο βάρος...)
Για να αντιμετωπιστεί αυτή η δυσκολία προχωρήσαμε στο εξής: Αφού κάθε λέξη αποτελείται από συγκεκριμένο αριθμό γραμμάτων, που έχουν ένα συγκεκριμένο άθροισμα, τότε μπορούμε να βγάλουμε ένα "μέσο βάρος" της κάθε μιας, διαιρώντας το λεξαριθμικό της βάρος με τον αριθμό των γραμμάτων της.
Έτσι, αν διαιρέσουμε το 56,7 της λέξης "πατέρας" με τα 7 γράμματα που την αποτελούν έχουμε τον αριθμό 8,1. Κάνοντας το ίδιο με όλες τις λέξεις, παίρνουμε στην ελληνική γλώσσα τιμές μέσου βάρους που ξεκινούν από το 0,98 και φτάνουν μέχρι το 13,28 με μέσο όρο το 6,47. Τα υπόλοιπα στατιστικά δεδομένα (για όσους γνωρίζουν από στατιστική) αίνονται στον επόμενο πίνακα και παρουσιάζουν αρκετό ενδιαφέρον, καθώς αποδεικνύουν μια πολύ συμμετρική οργάνωση των γλωσσών, διαφορετική για κάθε μία. Η διαδικασία επαναλήφθηκε για 10.000 αγγλικές, γερμανικές, γαλλικές, ιταλικές και ισπανικές λέξεις με τα εξής αποτελέσματα.
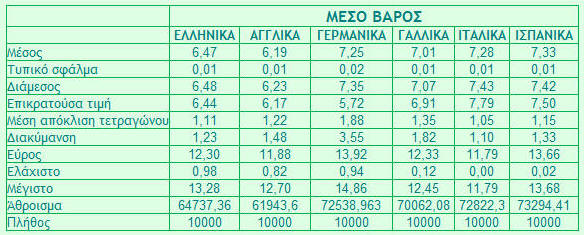
Για το τι σημαίνει αυτή η οργάνωση για την κάθε γλώσσα θα αναφερθούμε στη συνέχεια. Πρώτα ας δούμε τι ακριβώς γίνεται αν ελέγξουμε λέξεις με το ίδιο "μέσο λεξαριθμικό βάρος".
Ελέγχοντας, λοιπόν, τις λέξεις που έχουν ίδιο "μέσο λεξαριθμικό βάρος" παρατηρήσαμε ορισμένες ενδιαφέρουσες συμπτώσεις. Για παράδειγμα οι λέξεις "Θεός", "αναστηλώνω", "αθώρητος", "δυναμικός" "τελειοποιώ" και "μήτρα" βγάζουν όλες μέσο βάρος 6,52! Είναι εντυπωσιακό, διότι είναι ολοφάνερο ότι αυτές οι λέξεις μπορούν να ενοποιηθούν σε ένα κοινό "πνευματικό" ή "μεταφυσικό" υπόβαθρο.
Το κακό όμως είναι ότι, εκτός από αυτές, το ίδιο μέσο βάρος έχουν και οι λέξεις... "ντουβάρι", "βαγόνι" και μερικές ακόμη. Πώς θα γινόταν να βρεθεί ένας τρόπος ώστε να ξεχωριστούν αριθμολογικά κάποιες "τέλειες" λέξεις; Λέξεις δηλαδή που βάσει κάποιας τεχνικής θα συνδέονταν με έναν κοσμικό αριθμό, ένα νούμερο που όσο πιο αντικειμενικά γίνεται να υποδηλώνει τη σοφία του σύμπαντος, τον αλληλοσυσχετισμό ανάμεσα στις τέλειες αναλογίες κτλ., κτλ;
Υπάρχει τέτοιος αριθμός; Μα και βέβαια! Ο ίδιος ο Πυθαγόρας τον είχε ανακαλύψει και είχε μαγευτεί από τις ιδιότητές του. Πρόκειται για τον χρυσό αριθμό φ, αυτόν τον οποίο όλοι οι αρχιτέκτονες, οι γιατροί και οι μουσικοί μαθαίνουν στο πρώτο έτος των σπουδών τους και ονομάζεται χρυσή τομή, χρυσός λόγος, θεία αναλογία και έχει σαγηνεύσει τους μαθηματικούς εδώ και δυόμιση χιλιάδες χρόνια και για τον οποίο διαβάσατε παραπάνω, όσοι είχατε την υπομονή να το κάνετε!
Η ιδέα είναι η εξής: Αφού κάθε λέξη χαρακτηρίζεται από το μέσο λεξαριθμικό της βάρος, το οποίο ήδη περιγράφει μια σχέση της με το σύνολο της γλώσσας και τα συχνότερα χρησιμοποιούμενα γράμματα, αν αυτό το βάρος το διαιρούσαμε με τον αριθμό φ, δηλαδή το 1,618, θα βρίσκαμε πόσες φορές μεγαλύτερο είναι το μέσο βάρος από το φ. Αν η διαίρεση είναι τέλεια, τότε η λέξη θα μπορούσε επίσης να χαρακτηριστεί "τέλεια", καθώς ο,τιδήποτε είναι ακριβές πολλαπλάσιο του φ, εμπεριέχει μια "δόση" τελειότητας, όπως παραδέχονται οι πάντες!!!
Επιστροφή στην αρχή της σελίδας
Έβαλα λοιπόν πάλι όλα τα στοιχεία στο Excel, έδωσα την κατάλληλη συνάρτηση, και στη συνέχεια ταξινόμησα τις 10.000 λέξεις που είχα στη διάθεσή μου με βάση το μέγεθος του υπολοίπου που μένει αν διαιρεθεί το μέσο βάρος κάθε λέξης με το φ! Και εκεί άρχισαν τα περίεργα...
Ας δούμε πώς έγινε ακριβώς: Ας πάρουμε για παράδειγμα τη λέξη "θεός". Αθροίζοντας τα ψηφία βρίσκουμε βάρος 26,07. Διαιρώντας με τα 4 γράμματα της λέξης βρίσκουμε 26,07:4=6,518. Αυτό είναι το μέσο βάρος. Διαιρώντας το με το φ έχουμε 6,518:1,618=4,028430160692213. Επειδή το δεκαδικό μέρος συνήθως είναι πολύ μεγάλο και δυσκολεύει τους υπολογισμούς, αλλά και για να επιτευχθεί μια ομοιομορφία, αποφάσισα να στρογγυλοποιώ τα αποτελέσματα στο πρώτο δεκαδικό ψηφίο. Καθώς το φ είναι έτσι κι αλλιώς άρρητο, (όπως είναι και το γνωστό π=3,14.. ) η στρογγυλοποίηση κρίνεται αναγκαία.
Έτσι λοιπόν, το αποτέλεσμα της διαίρεσης του μέσου βάρους της ελληνικής λέξης "θεός" με τον αριθμό φ, είναι 4,0 πράγμα που σημαίνει ότι με τον δικό μου τρόπο αριθμολογικής ανάλυσης, η λέξη "θεός", είναι ακριβές πολλαπλάσιο του χρυσού αριθμού φ και κατά συνέπεια αποτελεί μια "τέλεια" λέξη.
Αν κάνουμε τις ίδιες πράξεις για τη λέξη "σύμπαν", έχουμε βάρος 38,66, μέσο βάρος 38,66:6=6,443 και αποτέλεσμα διαίρεσης με το φ, 6,443:1,618 = 4,0 !!! Συμπέρασμα: Και το "σύμπαν" είναι τέλεια λέξη στα ελληνικά, όπως ο "θεός"!!! Εντυπωσιακό σωστά;
Επίσης η λέξη "άγγελος" έχει βάρος 45,77, μέσο βάρος 6,539 και ΜΒ προς φ πάλι 4,0 !!!
Επίσης η λέξη "αγαθός" έχει βάρος 48,67, μέσο βάρος 8,112 και ΜΒ προς φ 5,0 !!!
Κατά συνέπεια, αφού το δεκαδικό μέρος είναι 0, σημαίνει ότι όλες αυτές οι λέξεις είναι ακριβή πολλαπλάσια του φ και κατά συνέπεια "τέλειες" λέξεις.
Συνεχίζουμε: Η λέξη "κόλαση" έχει βάρος 43,24, μέσο βάρος 7,207 και αποτέλεσμα διαίρεσης του ΜΒ με το φ 4,5. Η λέξη "διάβολος" έχει βάρος 56,67, μέσο βάρος 7,084 και αποτέλεσμα διαίρεσης του ΜΒ με το φ 4,4. Η λέξη "εξαποδώ" έχει βάρος 39,42, μέσο βάρος 5,631 και ΜΒ προς φ 3,5. Στις τρεις αυτές περιπτώσεις το δεκαδικό μέρος των πηλίκων των διαιρέσεων με το φ, είναι 5, 4 και 5 αντίστοιχα. Αυτό σημαίνει ότι απέχουν πολύ από το να είναι ακριβή πολλαπλάσια του φ, και άρα δεν είναι "τέλειες" λέξεις... Αυτό κι αν είναι εντυπωσιακό!!!
Γενικά ακολουθήθηκε η εξής πρακτική: Αν το δεκαδικό μέρος του αποτελέσματος της διαίρεσης του μέσου βάρους προς το φ είναι 0, η λέξη θεωρείται τέλεια, ότι περιέχει δηλαδή κάποιο ιδιαίτερο μεταφυσικό νόημα καθώς αποτελεί ακριβές πολλαπλάσιο του χρυσού αριθμού καθώς και ότι εκφράζει ένα τμήμα της τελειότητας της ελληνικής γλώσσας. Αν το δεκαδικό μέρος του αποτελέσματος της διαίρεσης του μέσου βάρους προς το φ είναι 1 ή 9 αυτό σημαίνει ότι η σχέση με το φ, δεν είναι άμεση αλλά οπωσδήποτε βρίσκεται πολύ κοντά στην τελειότητα. Συνακόλουθα εάν είναι 2 ή 8 θεωρείται αρκετά τέλεια, εάν είναι 3 ή 7 θεωρείται αρκετά ατελής, αν είναι 4 ή 6 σχεδόν ατελής και αν είναι 5 θεωρείται ατελής.
Για να απλοποιηθούν τα πράγματα ακολουθήθηκε η εξής διαδικασία: Αν η λέξη είναι τέλεια, αν δηλαδή το Μέσο Βάρος της είναι ακριβές πολλαπλάσιο του φ, τότε της δίνεται ως "βαθμός τελειότητας" ένα άριστα ίσο με 5. Αν είναι πολύ κοντά στην τελειότητα (δηλ. δεκαδικό μέρος του πηλίκου ΜΒ προς φ, 1 ή 9), τότε παίρνει έναν βαθμό 4. Συνεχίζουμε έτσι μέχρι το τέλος και η πιο ατελής λέξη, δηλαδή αυτή που έχει δεκαδικό μέρος της διαίρεσης ΜΒ προς φ ίσο με 5, τότε αυτή παίρνει βαθμό 0.
Πότε όμως δυο λέξεις δένουν καλά μεταξύ τους; Φυσικά αν είναι και οι δύο "τέλειες" δεν υπάρχει πρόβλημα. Ταιριάζει όμως ο "Μανόλης" με την "Κατίνα"; Ή ταιριάζει η "Μαρία Σπυροπαπαδοσπυράκη" με τη λέξη "κομμώτρια", ώστε να δει αν της πάει το επάγγελμα; Ή ταιριάζει το δικό σας όνομα με την έκφραση "να κερδίσω το λόττο";
Για να δούμε αν συνδυάζονται καλά δύο λέξεις ή εκφράσεις, προσθέτουμε το βαθμό τελειότητάς τους, (δηλαδή από 0 ως 5) και ελέγχουμε το άθροισμα. Το άθροισμα αυτό μπορεί να είναι από 0 ως 10, αφού για παράδειγμα αν έχουμε τις δύο τέλειες λέξεις "θεός" και "άγγελος" θα βγάλουν 5+5=10, ενώ αν έχουμε τις λέξεις "πόνος" και "φόνος" θα μας βγάλει άθροισμα 2, καθώς ο βαθμός τελειότητας κάθε μιάς είναι 1. Έτσι ο συνδυασμός βαθμολογείται σε μια κλίμακα 0 - 10 και μπορούμε να βγάλουμε ορισμένα συμπεράσματα.
Όμως συμβαίνει και κάτι άλλο: Μπορεί οι λέξεις να είναι ατελείς, ο συνδυασμός τους όμως να είναι πολύ ταιριαστός διότι ακόμα και ο "φόνος" ταιριάζει με το "πόνος", αφού έχουν και οι δύο βαθμό τελειότητας 1, παρ' όλο που ο βαθμός αυτός είναι μικρός. Δυο λέξεις δηλαδή μπορεί να ταιριάζουν μεταξύ τους, αλλά να μην είναι τέλειες, όπως ακριβώς συμβαίνει και με τους ανθρώπους. Δυο άνθρωποι έχουν τις ατέλειές τους και όμως όταν γίνουν ζευγάρι ο ένας να ακυρώνει τις ατέλειες του άλλου και μαζί να λειτουργούν άψογα!
Και για το τέλος, ας δούμε τι ρόλο παίζει ο αριθμός φ σε κάθε γλώσσα ξεχωριστά:
Κάνοντας μια μικρή αναγωγή των παραπάνω στα σύνολα των στατιστικών στοιχείων των διαφόρων γλωσσών προέκυψε το εξής εντυπωσιακό που θα ενθουσιάσει τους απανταχού ομιλούντες την Ελληνική! Ποιο είναι αυτό; Η ελληνική είναι η πιο "τέλεια" γλώσσα, σε σχέση με τον αριθμό φ! Κι αυτό διότι συμβαίνει το εξής: Το πηλίκο της διαίρεσης του μέσου όρου των "μέσων βαρών" όλων των λέξεων της ελληνικής γλώσσας που είχα στη διάθεσή μου (6,4 δες παραπάνω πίνακα) προς το φ είναι ακέραιος αριθμός, που σημαίνει ότι ο ΜΟ των μέσων βαρών των ελληνικών λέξεων είναι ακριβές πολλαπλάσιο του 1,6 δηλαδή του χρυσού αριθμού φ (1,6 χ 4 = 6,4)!!!
Το ίδιο συμβαίνει και με την αριθμητική διάμεσο των μέσων βαρών αλλά και την επικρατούσα τιμή καθώς τα αποτελέσματα της διαίρεσης είναι 4,01 και 3,98 αντίστοιχα! Συγκρίνοντας τα πηλίκα των διαιρέσεων των μέσων βαρών των λέξεων των άλλων γλωσσών, έχουμε τα εξής:

Όπως βλέπετε ΜΟΝΟ στα ελληνικά, αυτές οι τιμές είναι ακριβή (ή σχεδόν ακριβή) πολλαπλάσια του φ! Στις άλλες γλώσσες υπάρχουν σημαντικές διαφορές. Ιδιαίτερα εκείνες που το δεκαδικό μέρος είναι κοντά στο 50 είναι οι πιο απομακρυσμένες από το φ, και κατά συνέπεια, σύμφωνα με αυτή την οπτική οι πιο ατελείς. Μετατρέποντας τους αριθμούς αυτούς σε "ποσοστά τελειότητας", όπου η πιο τέλεια γλώσσα είναι αυτή που έχει μέσους όρους των παραπάνω στατιστικών στοιχείων πλησιέστερα σε πολλαπλάσιο του φ, παίρνουμε τα παρακάτω αποτελέσματα. Η σύμβαση είναι η εξής: δεκαδικό μέρος ίσο με 50 σημαίνει 0% τελειότητα, δεκαδικό μέρος ίσο με 0 σημαίνει 100% τελειότητα, 90 ή 10 σημαίνει 90% τελειότητα κοκ.

Και περνώντας τα δεδομένα σε γράφημα διακρίνεται ξεκάθαρα η υπεροχή της γλώσσας μας, η οποία φαίνεται να είναι η πιο δομημένη αριθμολογικά, καθώς και οι τρεις στήλες φτάνουν το 100%, και ακολουθούν οι υπόλοιπες γλώσσες ως εξής:
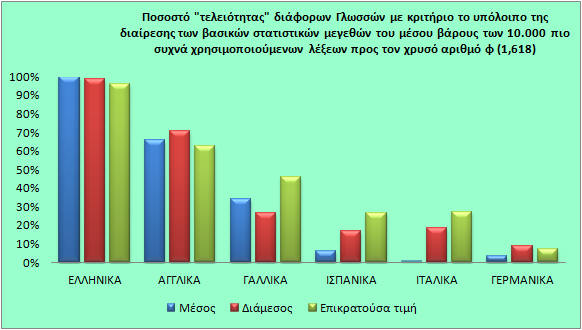
Αυτά λοιπόν στο θεωρητικό μέρος. Τώρα μπορείτε να ξαναγυρίσετε στην αρχή της σελίδας, να ασχοληθείτε με το πρόγραμμα-παιχνίδι, το οποίο ελέγχει τα αριθμολογικά δεδομένα όπως προτείνονται σε αυτή τη σελίδα και είμαι σίγουρος πως θα σας φάει πολλή ώρα καθώς ο μόνος περιορισμός είναι η φαντασία σας. Μπορείτε να μου στείλετε μέηλ αν βρείτε κάτι εξαιρετικά ενδιαφέρον, γιατί όπως είναι φυσικό, δεν ήταν δυνατό να ελέγξω μόνος μου όλους τους συνδυασμούς και δεν είχα στη διάθεσή μου όλες τις λέξεις.
Φυσικά δεν πρέπει να είστε τόσο εύπιστοι ώστε να στηρίξετε αποφάσεις ζωής πάνω σε αυτούς τους συνδυασμούς. Ξέρετε καλά ότι η αριθμολογία δεν είναι ακόμη ακριβής επιστήμη και εδράζεται μόνο σε αποσπασματικές παρατηρήσεις. Μέχρι να γίνει αποδεκτή (και ως εκ τούτου να κερδίσω το Νόμπελ), πάρτε μόνο κάποια ιδέα και σκεφτείτε πάνω στις σχέσεις σας με τους άλλους.
Σημείωση: Το κείμενο αυτό είναι πρωτότυπο και διατηρώ
κάθε επιφύλαξη για τα νόμιμα πνευματικά του δικαιώματα.
Δημοσιεύτηκε για πρώτη φορά στο διαδίκτυο την 11-11-11.
Εξυπακούεται ότι επιτρέπονται βιβλιογραφικές αναφορές
Διον. Παρούτσας
ΣΥΝΟΠΤΙΚΟΣ ΧΑΡΤΗΣ ΤΟΥ ΣΑΪΤ
Αυτό το σάιτ χρησιμοποιεί Κώδικα Καταγραφής (ΚωΚ ή cookies) κυρίως για την προβολή διαφημίσεων από την Google - Μάθετε περισσότερα...